Knowledge as Art: Chance, Computability, and Improving Education
Savants of Design
- “A man provided with paper, pencil, and rubber, and subject to strict discipline, is in effect a universal machine.” –Alan Turing.
The new science and experimental artistic philosophy of Thomas Bayes, Alan Turing, and George Maciunas share a fundamental unity in seeking the nodes, connecting lines, and points of intersection in a complex mass of relationships. Their alternative visions reveal a beautiful, pragmatic, and universal interconnectedness in viewing the world through its living networks. The theories of these creative geniuses, which sought to diagrammatically organize the factual clusters of the universe, are each aesthetics of organization and methodology.
Through their theoretical work, these visionaries developed new modes of understanding in mathematics and the arts which in turn, reveal deeper epistemological insights into understanding knowledge itself. Their graphic and theoretical language impart a new form of communication to divulge the complexity of their ideas. On diagrams, which he designates as “abstract machines”, Gilles Deleuze writes, “the diagram is a map, or rather, several superimposed maps… of relations between forces, a map of destiny, or intensity, which… acts as a non-unifying immanent cause which is coextensive with the whole social field.” Deleuze’s “abstract machine” lends its definition to the multifaceted nature of their philosophy and its infinite applications. As designers of design, these three individuals profoundly shifted the epistemological paradigms that determined Western comprehension of the world.
Fortuitous Learning: Initial Belief + New Data ->
Improved Belief
- “It is remarkable that a science, which commenced with the consideration of games of chance, should be elevated to the rank of the most important subjects of human knowledge.” –Pierre-Simon Laplace
From Pierre de Fermat and Blaise Pascal’s conception of probability theories in the 17th century, methodologies drawn from statistical reasoning generated new relationships between knowledge and free will. Presbyterian minister by day and mathematician by night, Thomas Bayes discovered a new kind of probability in the 18th century which was published posthumorously in the “Doctrine of Chances” by his friend Richard Price. Bayes’ Theorem was independently rediscovered by Pierre-Simon Laplace in the late 18th century and developed by Harold Jeffreys in his “Theory of Probability” in 1939. Like Presbyterianism’s debut into a Roman Catholic culture, this wealthy Englishman’s theory was viewed as controversial and nonconformist from its inception.

Bayes' Theorem “Given the number of times on which an unknown event has happened and failed: Required the chance that the probability of its happening in a single trial lies somewhere between any two degrees of probability that can be named.” --Thomas Bayes, “Doctrine of Chances” “The Bayesian approach, in which the arguments A and B of the probability operator P(A|B) are true-false propositions (with the truth status of A unknown to you and B assumed by you to be true), and P(A|B) represents the weight of evidence in favor of the truth of A, given the information in B.” --Professor David Draper
Bayes’ Theorem, an elegant statistical theory, provided a versatile way of optimizing one’s supposition to reach an accurate prediction: as more data is added, the accurate predictions become reinforced and the inaccurate ones rejected. Rather than determining effects from causes, Bayes reversed the order of conditioning to develop a theorem that determines causes from effects. As the method begins with a guess, mathematicians have regarded its stance on probability to be related to a degree of belief. The statistical process of calibration, brought into Bayesian practice by means of decision theory, has turned this paradigm into an approach that is logically sound.
Except for a handful of closeted practitioners, Bayes’ Theorem was historically regarded as a degenerate form of pseudoscience. For intellectuals such as John Stuart Mill, who denounced probability as “ignorance… coined into science”, it was difficult to accept that reason, the foundation of Western knowledge, could be subjected to something as whimsical as a guess. Given the dominance of the enlightenment paradigm which extolled the fanatical collection of objective facts through empirical measurement, scientists throughout history regarded Bayesianism as “subjectivity run amok”.
Despite its reputation, Bayesian probability enabled scientists to approach one time events and situations about which they had little prior information, feats impossible under the dictates of frequentism. Bayes’ Theorem has been used to calculate the masses of planets, set up the Bell phone system, set up the United States’ first working social insurance systems, and was even used to accurately predict the winner of the presidential race between Nixon and Kennedy in forty-nine states. However, long associated with negative ideological connotations, Bayesian techniques were covertly used under the guise of other names. Only recently has Bayes’ Theorem come into the open.
Its use was also overshadowed by its rival theory, Frequentism, which was established as the orthodox statistical method in 1925 by Ronald Fisher. The frequentist, or the relative-frequency approach, restricts attention to hypothetical repetitions which assumes phenomena is inherently repeatable under ‘identical’ circumstances. In essence, frequentist ‘objectivity’ supposes that “two scientists with the same data set should reach exactly the same conclusions”. The Bayesian approach combines information both internal and external to the data set and relies on integration instead of maximization, requiring all relevant information to bear on the calculation. In essence, Bayesian inference supposes that the role of science is to accumulate knowledge and reach new conclusions that are synthesized with previous information. In his lecture on Bayes Theorem, UC Santa Cruz Professor David Draper remarks that Bayesian inference follows the standards of rigorous mathematics: “There’s a logical progression from principles, axioms, to a theorem that says this [Bayesian interpretation] is the only way to quantify uncertainty that does not violate principles of internal logical consistency.”
The use of frequentist or Bayesian approaches has been one of the greatest controversies in statistics in the 20th century and the differences between the two approaches are still widely misunderstood today. In his paper, “The Promise of Bayesian Inference for Astrophysics”, Cornell Professor Thomas Loredo says that the two approaches are misunderstood as having ‘merely philosophical’ differences or for producing different results only in certain circumstances. The Bayesian paradigm is profoundly and fundamentally different from its counterpart –so much so that the Bayesian inference has been regarded as “a separate paradigm, distinct from their own, and merely… think of it as another branch of statistics, like linear models”. In Professor Loredo’s comparisons of two approaches, he concluded “frequentist methods to be fundamentally flawed” and Bayesian techniques to straightforwardly overcome these problems based solely on their performance.
The revival of Bayes’ Theorem has led to a ‘Bayesian revolution’ in a wide range of fields including medical diagnosis, ecology, geology, computer science, artificial intelligence, machine learning, genetics, astrophysics, archaeology, psychometrics, education performance, sports modeling, among others. Dr. Greg von Nessi, a researcher studying fusion power, modelled the behavior of plasmas using Bayesian inference. On Bayesian methods, Dr. Nessi says, “the beauty of this approach is that you don’t have to deal directly with the hugely complex interdependencies within the data but those interdependencies are automatically incorporated into the model”. As less assumptions are built into the initial model, Bayesian inference allows its practitioners to study the patterns of complex systems and the interaction of their measurements.
Analogous to human learning processes, Bayesian inference allows its practitioners to generate ideas by continuously modifying the extent of their scientific belief or expectations. As a methodology, Bayesian techniques offer a means to comprehend data by perpetually reducing human error through experience. In effect, it is possible to interpret prodigious amounts of data and merge the information in a globally consistent manner. In essence, the Bayesian paradigm encapsulates an ideology of education as a learning model which builds upon chronological history of ideas. As professor Draper remarks in his lecture, “It moves toward a world in which we’re trying to embrace all possibilities and let the data pick out the good ones”.
Bayes’ Theorem was also used in the cryptoanalytic work of British mathematician Alan Turing to decipher the uncrackable ‘enigma code’ during World War II, a feat which arguably saved the Allies from losing the war. By using Bayesian techniques to test and eliminate different code probabilities, Turing was able to narrow the scope of probability down to decipher the German messages. In doing so, he conceived of the “ban”, defined as “the smallest change in weight of evidence that is directly perceptible to human intuition”. Developed coterminously with the “bit”, these ‘infinitesimals’, indefinitely small measurements, were fundamental to the development of the Bell telephone systems and modern computers.
Turing’s work with Bayesian inference laid the groundwork for the Turing Machine, a hypothetical model of the process of computation developed with the aim to capture the process of the human mind when carrying out a procedure. Modelled on a teleprinter, the operation of the machine is determined by a finite set of deterministic mechanical rules which causes it to move, print, and halt. Though the Turing Machine itself is a simple abstract model, it is significant in that Turing was the first to conceive of the machine as a model for computation in 1936. In essence, the Turing machine captures the modern computer’s table of behavior in its most elementary form and encompasses the most fundamental notion of ‘method. His formulation of ‘computability’ extends further in his concept of a Universal Turing Machine, a Turing Machine which can simulate other Turing Machines. This model, considered by New York University Professor Martin Davis as the origin of the stored computer program, proposes that anything which is computable can be computed by this conceptual machine.
Turing also explored the possibility of ‘uncomputable numbers’ in his Princeton Phd thesis, “Systems of Logic based on Ordinals” (1938), in reformulating Kurt Godel’s work on the limits of proof and computation. Godel’s Theorems of Incompleteness demonstrates that there is no formal logic system that can be both consistent and complete because there will always be some propositions which cannot be proven true or false using the rules and axioms within a logical arithmetic system. Essentially, Godel’s theorems suggest that all logic suffers from incompleteness and no consistent axiomatic theory can prove its own consistency.
In turn, Turing developed ordinal logic, a recursive method so that from a given system of logic, a more complete system may be constructed. Turing also conceived of the Oracle Machine, a Turing Machine connected to an entity called the ‘oracle’ which which is able to resolve decision problems like the Halting problem in the Turing Machine. The oracle, infinitely more powerful than a computer, is able to resolve uncomputable operations and explores the realm of what can be computed by purely mechanical processes. Turing work’s has not only opened a spectrum of new innovations in practical computation, but in philosophical discussions on cognition and the design of the human brain as well.

Turing Machine
The applications of the Turing Machine and Bayesian techniques are consonant with building rigorous mathematical models that imitate the relational schema in extraordinarily sophisticated systems. The Turing Machine and Bayesian inference have greatly contributed to the field of machine learning, a branch of artificial intelligence concerned with the design of algorithms that allow computers to evolve behaviors based on empirical data. As a means of creating complex programs, these theories are used to create models which are able to acquire and internalize new information as they encounter new scenarios. ‘Ensemble learning’, the development of supervised learning algorithms which makes its own predictions, is one such application which incorporates Bayesian techniques into Turing’s model.
Currently, these theories have found their application in economics to create financial models that learn and adapt to new information. As a “quant”, or “quantitative analyst”, Mahnoosh Mirgaemi finds patterns in a sea of electronic data to develop sophisticated financial products. Mirgaemi, who recently completed her doctoral thesis on the use of Bayesian techniques in financial markets, used Bayes’ theory to study how European bond markets respond to economic news reports. In all, Mirgaemi analyzed 3,077 pieces of economic data and 1.6 million bond trades to determine how news shifts the market. Conducive to large masses of data and states of constant flux, these theories accommodate vacillating systems in real time.
Bayesian inference, by deriving cause from effect, views the production of events from a cluster of independent causes rather than a linear line of reasoning. By making fewer ‘objective’ assumptions, the Bayesian perspective quantifies uncertainty with the belief that better conclusions will fortuitously emerge. Likewise, Turing explored principles of logic to develop a critical methodology that accommodates problems of incompleteness in human knowledge. Turing’s theories, exploring the black holes of computable processes, scrutinizes the limits of any logical systems of knowledge. In their processes to understand uncertainty and computability, these methodologies engage change as part of a learning process to analyze and develop the limits of the human knowledge processing.
George Maciunas: Sage of Fluxus
- “entia non sunt multiplicanda praeter necessitatem”
- entities should not be multiplied beyond necessity. –Occam’s Razor
Attributed to the 14th century English logician, Father William of Ockham, Occam’s razor is used as a heuristic to guide scientists in the development of theoretical models. Occam’s razor is a scientific rule of thumb which recommends forming a hypothesis that contains the fewest new assumptions. In relation to Laplace’s view of probability as an instrument for “repairing defects in Knowledge”, Occam’s razor is a methodological principle which suggests that scientists should begin with the clearest hypothesis and improve it with added data. The validity of this epistemological preference was supported in 2005, when computer scientist Marcus Hutter mathematically proved that shorter computable theories may hold more weight than their busy counterparts.
Clarity and efficiency were also part of the philosophy of Fluxus sage, George Maciunas, whose cohesive approach extended the arts into political spaces. Maciunas was an eternal student who obtained multiple degrees in art history, graphic design, architecture, and musicology in higher education for eleven years. His interdisciplinary education contributed to his ability to diagrammatically conceive of experimental and pragmatic solutions geared for social transformation. Maciunas used his utopian resolve to meet the needs of society and merge art and life towards an ideal of unfragmented enlightenment. Fluxus, an art movement in the 1960’s, was a collective of artists, composers, and thinkers who shared these social and aesthetic visions.
Maciunas was highly critical of the stratified, standardized, and bureaucratic system of American education institutions, which he viewed to cause “premature specialization and fragmentation of Knowledge”. As he deduced such inefficiency to be caused by the slow ‘linear-narrative method’ of information processing found in books, lectures, film, and television, Maciunas proposed a new system of data presentation to assist in reforming education. His “Preliminary Proposal for 3-Dimensional System of Information Storage and Presentation” contends that linear information media would be better replaced by a diagrammatic three dimensional system of information storage and presentation as an learning tool. Maciunas’ philosophy not only proposed reforms of the educational status quo, but a war on Western culture to change epistemological paradigms and move towards a unified vision from a cross disciplinary approach.
The majority of Maciunas’ scholarly research in art history, focused on the European and Siberian art of migrations, reflects his devoted interest on the intersection between Eastern and Western epistemological paradigms. In his 1959 essay, “Development of Western Abstract Chirography as a Product of Far Eastern Mentality”, Maciunas explores a concept which he calls “cyclic periodicity” to propose that an ideological shift in Western and Eastern mentalities occurs every millennium between the two trains of thought. Maciunas associates the Western mentality with a belief in “humanistic, relative and rational truth”, while the Eastern mentality embodies “spiritual absolute realism, and unity of form and content”. A proponent of the abstraction in the Eastern mentality, he says, “one must perceive and express the universe with one stroke”. In this context, he writes of abstract chirography, a form of handwriting, to display an “abstract beauty of character… capable of drawing the mind away from literal meaning” and to be indicative of a current millennial shift towards Eastern philosophies. He proposes that the West is currently experiencing a period of decline due to the cultural degeneration brought on by the progress launched by free will and reason. In effect, Maciunas suggests that Western ideals have caused a decomposition of its institutions.
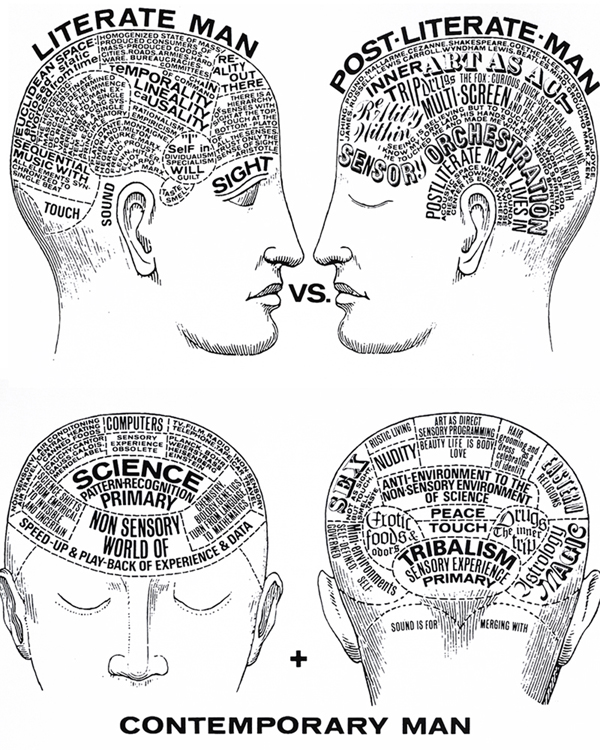
Contemporary Man
Maciunas’ set of paintings from the 1950’s reflect the pantheistic nature of the Eastern Mentality to view the universe and God as one and the same. These canvases, which combine aesthetics of the ancient Far East and the Western avant garde, evoke a nostalgic exploration of figuration and abstraction. Resting above a mountain landscape, the burning red sun in Painting I is reiterated as red and blue celestial spheres in Painting II and Painting III. Arboreal branches whimsically extend throughout the textured background in the latter paintings, traversing the black space in which the spheres levitate. These branch-like structures reference the fractal systems of the natural world in its abstract simplicity –each twig a self-similar structure of its larger branch. With the lack of a linear narrative, each painting represents a pure moment of structural unity in this relationship between fluxions, textured spaces, and bold figuration.
These paradigms of Eastern and Western mentality are also reflected in Maciunas’ work, “Contemporary Man”, which display the craniums of two figures, designated as ‘literate man’ and ‘post-literate man’, defined by a collection of words and phrases written within them in partitioned spaces. Expressions of language such as “euclidean space: enclosed – static divorced from time” and “science; pattern-recognition; primary” fill the mind of ‘literate man’, while the discourse of ‘post-literate man’ contain phrases such as “tribalism; sensory experience; primary” and “seeing is believing but to touch is the word of god”. Guided by the sense of sight and linear causality, the ‘literate man’ manifests objective knowledge and reason in his sense of self. His non-seeing counterpart, led by the faculties of touch and sound, experiences the world through belief and his own autonomy. These assemblages of text fragments delineate a fundamental divide between Maciunas’ concepts of ‘traditional man’ and the ‘new man’ of the millennial shift.
Akin to what may be described as their Bayesian and Frequentist counterparts, these two models of man also display particular processes which govern their actions. Analogous to Bayesian inference, Maciunas sums up the Eastern mentality with a statement by Tertullian, “I believe in order that I may know”. Tertullian’s statement exemplifies Bayesian inference by its order in which belief precedes knowledge. Reciprocally, Maciunas uses the words of Anselm the Scholastic to describe the Western mentality, “I would know in order that I may believe”. This statement may be seen as the equivalent to Frequentist approaches which, dependent on previous repetitions of the same event, displays the order that knowledge precedes belief.
Mirroring Eastern philosophies, Maciunas’ pictorial methods sought to express a model of unfragmented knowledge in diagrammatic form. On the graphological definition of chirography and Eastern Mentality, Maciunas writes, “the perception of the essential and the awareness of the universe is intuitive rather than rational, and immediate rather than analytical… the process of expression is one and the same as that of perception”. As Maciunas asserts that “individual will and reason must be submerged under the will and power of the absolute”, he proposes that Eastern chirography achieves ‘actus purus’, a spontaneous gesture freed from conscious effort culminating in unity. In essence, Maciunas’ paintings and his diagrams sought to culminate the particularities and generalities of knowledge processing to this ideal.
Prophets to a New Age
- “[Mathematics] is a landscape riddled with holes and paradoxes.
- It is a chaos filled not with reasons and whys,
- but with contradictions and why nots.” –Alan Turing
Symbolized through the language of numbers and diagrams, the conceptual models of Bayes, Turing, and Maciunas shift away from linear modes of thought towards multidimensional networks. Like the organization of an ant colony, they express an economy of knowledge through the global communion of ideas. Apropos to Marshall McLuhan’s concept of the ‘global village’, these theories essentially prophesized the conceptual backbone of mass data systems like the world wide web decades before their conception. Like Maciunas’ research on ‘cyclic periodicity’ and the Eastern Mentality, McLuhan’s famous aphorism was coined to describe the new social organization that will form when Western paradigms shift from a fragmented individualism to a collective identity with a “tribal base”, and when visual culture will be replaced by its aural equivalent. Today, it is used as a term to describe the internet.
McLuhan, who also developed this concept in the early 1960’s, predicted the internet’s information processing as such: “A computer as a research and communication instrument could enhance retrieval, obsolesce mass library organization, retrieve the individual’s encyclopedic function and flip into a private line to speedily tailored data of a saleable kind”. Fundamentally, Maciunas’ ideals of speed and pragmatism resonate with this prophetic statement in his “Learning Machine”, a model which represents the shift from a two-dimensional to three-dimensional form of knowledge storage and communication. Maciunas, who envisioned a collectivist utopia in his artistic agenda, unified this concept with his radical and humanitarian solutions.
Maciunas' Learning Machine
On diagrams, or ‘abstract machines’, Gilles Deleuze writes, “The abstract machine is like the cause of the concrete assemblages that execute its relations; and these relations take place ‘not above’ but within the very tissue of the assemblages they produce”. As alternative theorists, what Bayes, Turing, and Maciunas shared in common was a penchant for understanding the intuitive connections between a model and its process. In principle, Bayes and Turing moved towards a new mathematics to understand the processes of God, intelligence, and the universe, and Maciunas founded a new art to express its ideology in his aesthetic of administration. Unified by their universality, these ‘learning machines’ sought to comprehend the relational schema inherent to constructive processes and offer a resolution through education. As their paradigms engaged the very essence of what a structure is, the theories of these three geniuses fused various facets of knowledge and administration into globally consistent models of learning. As solutions to understanding uncertainty, computability, and learning, these models reflect a dramatic transformation in Western epistemological paradigms of knowledge processing.
Bibliography
Barker-Plummer, David, “Turing Machines”, The Stanford Encyclopedia of Philosophy (Spring 2011 Edition), Edward N. Zalta (ed.),
URL = <http://plato.stanford.edu/archives/spr2011/entries/turing-machine/>.
Bayes, Thomas. “Doctrine of Chances by Thomas Bayes.” George Maciunas Foundation Inc.. N.p., n.d. Web. 23 Mar 2012.
<http://fluxusfoundation.com/?page_id=408>.
“Bayesian Inference of Fusion Plasma Parameters.” Plasma Research Laboratory. The Australian National University, n.d. Web. 23 Mar 2012.
<http://prl.anu.edu.au/PTM/Research/Bayesian/>.
Bertsch, Sharon, perf. The Theory That Would Not Die” How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines, and Emerged Triumphant from Two Centuries of Controversy. AtGoogleTalks, 2011. Web. 23 Mar 2012.
<http://georgemaciunas.com/?page_id=2793>.
Copeland, B. Jack, “The Church-Turing Thesis”, The Stanford Encyclopedia of Philosophy (Fall 2008 Edition), Edward N. Zalta (ed.),
URL = <http://plato.stanford.edu/archives/fall2008/entries/church-turing/>.
Gillispie, Charles Coulston. Pierre-Simon Laplace, 1749-1827: A Life in Exact Science. Princeton: Princeton University Press, 1997. 3-18. Web.
<http://books.google.com/books?id=iohJomX0IWgC&printsec=frontcover&dq=inauthor>
<http://books.google.com/books?id=iohJomX0IWgC&printsec=frontcover&dq=inauthor> :”Charles Coulston Gillispie”&hl=en&sa=X&ei=XsBsT5GYMKXz0gGH-9TzBg&ved=0CEEQ6AEwAQ
Hubert, Christian. “diagram / abstract.” Christian Hubert Studio. Christian Hubert, n.d. Web. 23 Mar 2012.
<http://www.christianhubert.com/writings/diagram___abstract.html>.
Knight, Sam. “School for quants: Inside UCL’s Financial Computing Centre, the planet’s brightest quantitative analysts are now calculating our future .” Financial Times Magazine. 02 Mar 2012: n. page. Web. 23 Mar. 2012.
<http://www.ft.com/intl/cms/s/2/0664cd92-6277-11e1-872e-00144feabdc0.html>
Maciunas, George. “George Maciunas: A Research Essay on Development of Western Abstract Chirography as a Product of Far Eastern Mentality, N.Y.U. Institute of Fine Arts,1959.” George Maciunas Foundation Inc.. N.p., 1959. Web. 23 Mar 2012.
<http://georgemaciunas.com/?page_id=1344>.
Muehlhauser, Luke. “A History of Bayes’ Theorem.” Less Wrong: A community blog devoted to refining the art of human rationality. Singularity Institute, 29 Aug 2011. Web. 23 Mar 2012.
<http://lesswrong.com/lw/774/a_history_of_bayes_theorem/>.
Porter, Theodore M. The Rise of Statistical Thinking, 1820-1900. Princeton: Princeton University Press, 1986. 71-76. eBook.
<http://books.google.com/books?id=5a2a3jlBNb0C&printsec=frontcover&dq=inauthor>
<http://books.google.com/books?id=5a2a3jlBNb0C&printsec=frontcover&dq=inauthor> :”Theodore M. Porter”&hl=en&sa=X&ei=7bdsT4mdMePL0QGNpLHUBg&ved=0CDkQ6AEwAA
Schmidt-Burkhardt, Astrit. Maciunas’ LEARNING MACHINES From Art History to a Chronology of Fluxus. 1st ed. Berlin: The Gilbert and Lila Silverman Fluxus Collection Foundation, 2003. 7-27. Print.
Spade, Paul Vincent and Panaccio, Claude, “William of Ockham”,The Stanford Encyclopedia of Philosophy (Fall 2011 Edition), Edward N. Zalta (ed.),
URL = <http://plato.stanford.edu/archives/fall2011/entries/ockham/>.
Wikipedia contributors. “Marshal McLuhan.” Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, Web. 23 Mar 2012.
<http://en.wikipedia.org/wiki/Marshall_McLuhan>
© 2013 George Maciunas Foundation Inc., All Rights Reserved